
How good are Language Models at maths?
In the last years, large pretrained language models, like GPT, BERT, GPT-2 or GPT-3, have sparked a revolution in the field of Natural Language Processing, setting new standards in many tasks. These models allow researchers to leverage their large training data and expressive power to adapt them to new tasks with minimal or no training data. A nice survey on the subject can be found here.
These models learn how words relate to each other, the structure of sentences and documents and so on. They do not understand the text, have intelligence or threaten to enslave humankind just yet. They do, however, exhibit amazing capabilities. Today, we’ll see how good they are at doing maths.
The first test
We will evaluate the following models: BERT, RoBERTa, GPT-2 and different GPT-3 variants. To this end, we will ask them to perform operations of increasing difficulty:
-
For the Masked Language Models, our prompts will be in the form Two plus two equals [MASK]. The task of the model is to fill in the blank.
-
For the Causal Language Models, our prompts will be in the form Two plus two equals and the task of the model is to complete the sentence. In this case, it is important to set the temperature parameter to 0.0, since we want the model to always output the most likely answer.
For BERT, RoBERTa and GPT-2 models, we will use the Huggingface Transformers library, while, for the GPT-3 variants, we will use the OpenAI API. At the time of writing, this API exposes 4 GPT-3 variants aimed at text-generation; from smaller to larger: Ada, Babbage, Curie and Davinci.
The results of this first test are shown in the following table. For problems 1 to 17, we prompted the models as both Two plus two equals… and 2+2= and took the best answer. For the last problem, the prompt was: Solve for x: x-5=20. x =.
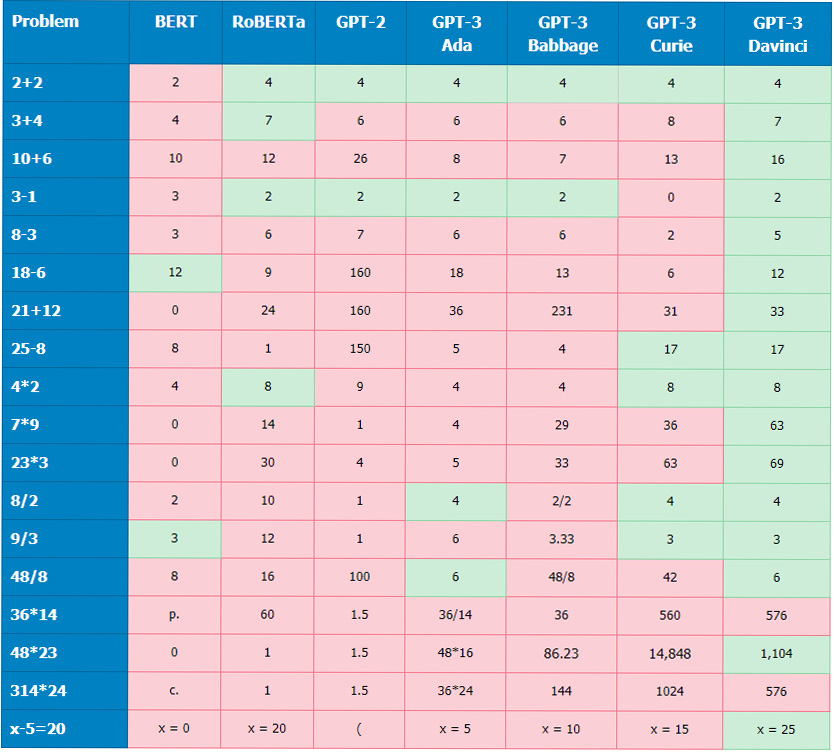
The performance of the previous-generation models, BERT, RoBERTa and GPT-2, is quite unimpresive, with RoBERTa seemig to be slightly better. It is clear that they are not good at maths.
For comparison purposes, my 5-year-old child got the first 8 right, so he is well above most of the models. Another victory for humankind 🏆. I prompted him in natural language, just like with the models. Note that he is not a native English speaker, but watching Numberblocks on YouTube goes a long way.
Not surprisingly, we need to move to the larger GPT-3 architectures to achieve good results. The ability to be prompted to perform arbitrary tasks is something that has only emerged with the large last-generation models. See for example this paper and the references therein.
Let’s see what else is GPT-3 capable of.
Final exam
We will now focus on GPT-3 Davinci and propose more challenging questions:
| Problem | Prompt | Answer |
|---|---|---|
| 1 | Solve for x: x^2 = 16. x = | 4 👍 |
| 2 | Solve for x: x^2 + 5 = 30. x = | 5 👍 |
| 3 | Solve for x: x^2-8x+15=0. x= | 3 👍 |
| 4 | Solve for x and y the following system of simultaneous equations: x+y=6, x-3y=2 | x=4, y=2 👎 |
| 5 | Given the function f(x)=x/3, f(6)= | 2 👍 |
| 6 | Simplify the following expression: 2^5*2^4 | 2^9 👍 |
| 7 | Simplify the following expression as a single power: \dfrac{2^5\cdot 2^4}{2^7} | \dfrac{2^{5+4}}{2^{7}} |
| 8 | Given the function f(x)=x^2 + 3x, f’(x)= | 2x + 3 👍 |
| 9 | Given the function f(x)=x^2 + 3x, is f(x) a linear function and why? | No, f(x) is not a linear function. 👍 |
I think these results are quite exciting. GPT-3 is capable of solving second-order equations, evaluating a function on a particular point, simplifying expressions and even computing derivatives.
In Problem 7, it did not reach the final solution, but we can see that performs correctly the first step. Moreover, it understands the LaTeX notation and continues to use it.
For Problem 8, it correctly computes the derivative of the proposed function and then follows with: The derivative of a function is the rate of change of the function with respect to the input variable. In this case, the derivative is 2x + 3, which means that the rate of change of the function is 2x when x is incremented by 1.
The full answer to Problem 9 was: No, f(x) is not a linear function. The graph of a linear function is a straight line, while the graph of f(x) is a curve. Which is true, but not so useful. The presence of the term x^2 would have been a better answer.
The only failure is at solving the system of equations and maybe the explanations of problems 8 and 9. I’m pretty sure, however, that this could be solved with more careful design of prompts.
Conclusions
This was my first time working with GPT-3 and I’ve been impressed. It really represents a departure from previous models, and these tests are not even the best example of their capabilities.
The older models, on the other hand, performed below my initial expectations. I assumed they would have at least very basic algebraic abilities. It is possible, however, that these results could improve to some extent by designing better prompts.
Going back to GPT-3, I’m really excited about its possibilities. The fact that it encodes so much information that it can be prompted instead of fine-tuned to perform any task is a real paradigm shift and get us closer to actual AI assistants. I’ll continue to play with it, so we will hopefully have the chance to discuss the topic in more depth.